A Beginners Guide to Big O Notation in Python

Sam LaFell

As someone who comes from a non-computer science background, I fell into Data Science, and then fell again into Python, which led me to Data Science. Sometimes, I wish I had taken the formal route of computer science, but most of the time, I’m thrilled with the path that has led me to where I am today.

But what does that mean? I lack some formal computer science training that would help me break into the next level, so I pursue this knowledge myself. Today, I want to introduce you all to a topic that I’ve been learning about recently.

Why should we care?
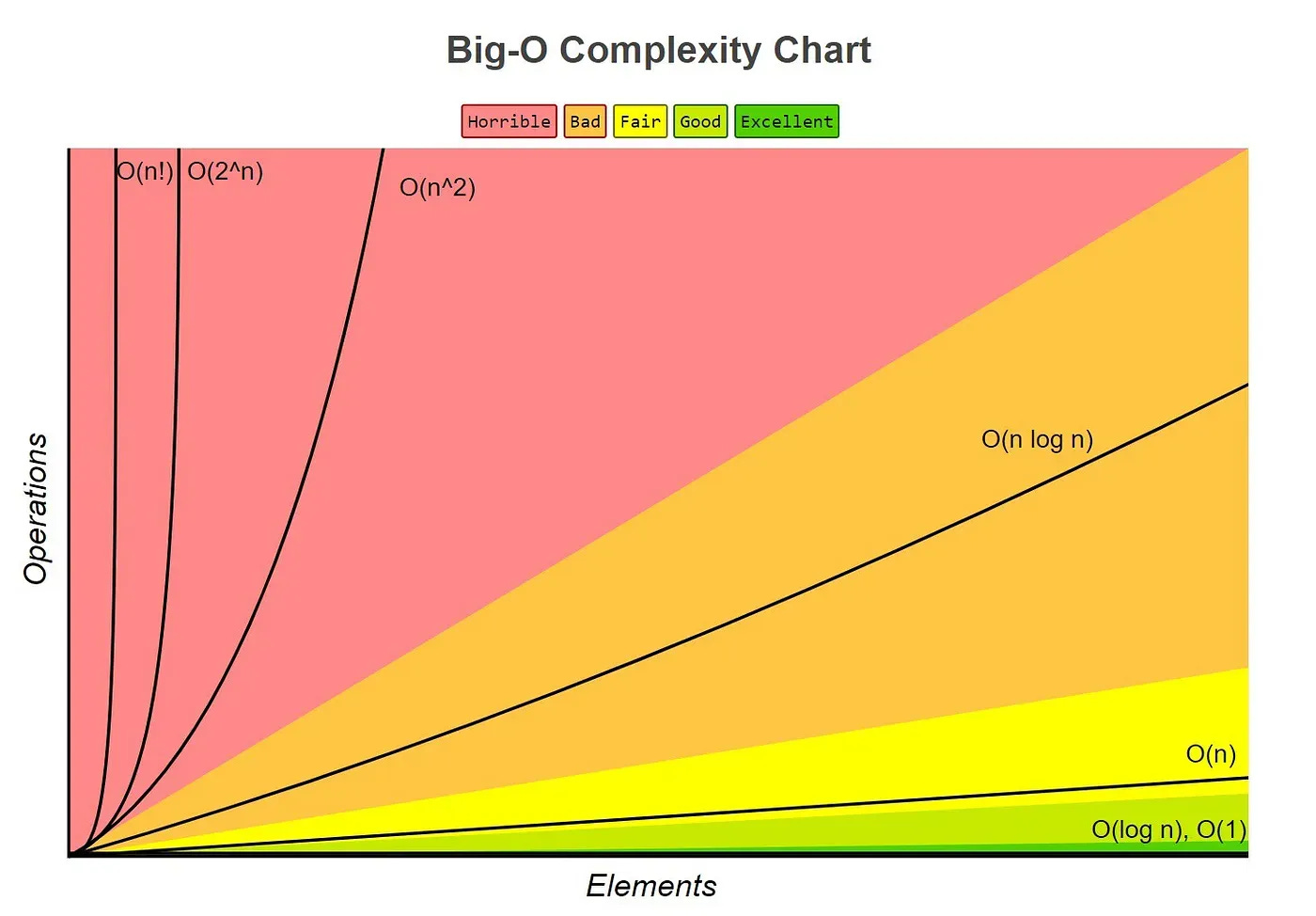
As a data scientist, it’s super important for us to have a good grasp of the Big O time complexity of our algorithms. This can help us optimize our code and make it run faster. By minimizing the time complexity of our algorithms, we can make our code more efficient, reduce the amount of time it takes to process large amounts of data, and ultimately improve the quality of our analysis. Keep up the great work!

Credit

When analyzing the efficiency of algorithms, it is important to understand how the amount of input data affects the computation time. A common way to express this is through Big O notation, which characterizes the worst-case time complexity of an algorithm in terms of the size of its input. Here are some common Big O time complexities and their meanings:

O(1)

• The algorithm takes constant time to complete, regardless of the size of the input data. An example of this is accessing an element in an array by its index.

def get_first_element(arr):
   return arr[0]

O(n)

• The algorithm takes time proportional to the size of the input data to complete. Examples of this include iterating through an array or searching for an element in an unsorted list.

def search_array(arr, x):   
	for i in range(len(arr)):      
    	if arr[i] == x:         
        	return i   
        return -1

O(n**2)

• The algorithm takes time proportional to the square of the size of the input data to complete. Examples of this include nested loops or bubble sort.

def bubble_sort(arr):

	n = len(arr)
    for i in range(n):      
    	for j in range(0, n-i-1):         
        	if arr[j] > arr[j+1] :            
            	arr[j], arr[j+1] = arr[j+1], arr[j]   
            	return arr

O(log n)

• The algorithm takes time proportional to the logarithm of the size of the input data to complete. Examples of this include binary search or certain divide-and-conquer algorithms.

def binary_search(arr, x):   
	low = 0   
    high = len(arr) - 1   
    mid = 0   
    while low <= high:      
    	mid = (high + low) // 2      
        if arr[mid] < x:         
        	low = mid + 1      
        elif arr[mid] > x:         
        	high = mid - 1      
        else:         
        	return mid   
        return -1

Understanding the Big O time complexity of your algorithms can help you optimize your code and improve its performance. By minimizing the time complexity of your algorithms, you can make your code more efficient and reduce the amount of time it takes to process large amounts of data.

So, when you are designing or analyzing an algorithm, remember to consider its Big O time complexity and strive to optimize it whenever possible.

Actually, I plan to share with you each of the major DS and Algos topics I learn about over the next few weeks. This is preparing me in line with my career goals, and I hope you all stick around to see some of the things I learn.